什么是二叉搜索树
二叉搜索树,顾名思义,其主要目的用于搜索,它是二叉树结构中最基本的一种数据结构。
如下图所示:
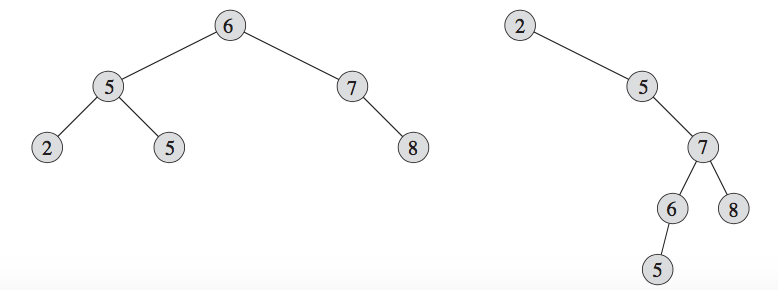
二叉搜索树中的关键字总是按照下面的方式存储:
设x为二叉搜索树中的一个节点,如果y是x左子树的一个节点,则y.key <= x.key;如果y是x右子树的一个节点,则y.key >= x.key。
二叉搜索树的遍历
中序遍历:左-根-右
上中图,两棵树的中序遍历均为2,5,5,6,7,81
2
3
4
5def inorder_tree_walk(x):
if x is not null:
inorder_tree_walk(x.left)
print x.key
inorder_tree_walk(x.right)
先序遍历:根-左-右
后序遍历:左-右-根
定理:如果x是一棵有n个子节点的根,那么调用inorder_tree_walk(x)需要O(n)时间。
查询二叉搜索树
查找:(小于节点在左树找,大于节点在右树找。)1
2
3
4
5
6
7def tree_search(x,k):
if x == null or k == x.key:
return x
elif k < x.key:
return tree_search(x.left,k)
else:
return tree_search(x.right,k)
最大最小:(最大的即找最右边的,最小即找最左边的,以最大为例)1
2
3
4def tree_max(x):
while x.right is not null:
x = x.right
return x
有时候需要按照中序遍历的次序查找某个节点的后继。分两种情况:
- 有右子树,那么查找x节点右子树上的最小值即可。
- 无右子树,并有一个后继y,那么y就是x的最底层祖先,并且y的左孩子也是x的一个祖先。例如,上图左边的树中5的后继节点为6。为了找到y,x开始沿树向上直到遇到这样一个节点:这个节点是它双亲的左孩子。
后继:1
2
3
4
5
6
7
8
9def tree_successor(x):
if x.right is not null:
return tree_min(x.right)
y = x.parent
while y is not null and x == y.right:
x = y
y = y.parent
return y
备注:这里用到了一个性质,如果T中一个节点x的右子树为空,且x有一个后继y,那么y一定是x的最底层祖先,并且其左孩子也是x的祖先。前驱类似,这里不再赘述。
以上操作时间复杂度均为O(h),其中,h为树的高度。
插入
将一个新值v插入到二叉搜索树T中,以节点z作为输入,其中z.key=value,z.left=null,z.right=null。这个过程需要修改T和z的某些属性,把z插入到相应的位置上。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18def tree_insert(T,z):
x , y= T.root , null
# x用来记录路径
while x is not null:
y = x
if z.key < x.key:
x = x.left
else:
x = x.right
# 用来记录要插入位置的父节点
z.parent = y
# 判断插入在何处
if y is null:
T.root = z
elif z.key < y.key:
y.left = z
else:
y.right = z
删除
从一棵二叉搜索树T中删除一个节点z,分为三种情况:
- z没有孩子,直接删除z,并修改父节点。
- z只有一个孩子,这个孩子代替z,并修改父节点。
- z有两个孩子,这种情况最复杂。
下面是四种情况:(一图胜千言)
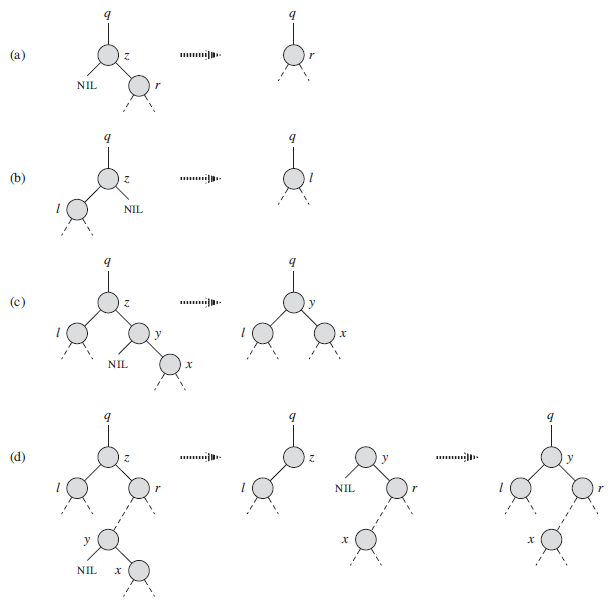
实际上所有的这些情况都是在执行移植的一个过程。现在我们来定义一下这个子过程transplant,它是用另一棵子树替换一棵子树并成为其双亲的孩子节点。
1 | def transplant(T,u,v): |
下面是二叉搜索树中删除节点z的过程:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20def tree_del(T,z):
# 没有左孩子
if z.left is null:
transplant(T,z,z.right)
# 没有右孩子
elif z.right is null:
transplant(T,z,z.left)
# 下面是有两个孩子的情况
else:
# 查找节点y
y = tree_min(z.right)
if y.parent != z:
# 上图情况(d)
transplant(T,y,y.right)
y.right = z.right
y.right.parent = y
# y替换z,上图情况(c)
transplant(T,z,y)
y.left = z.left
y.left.parent = y
参考书目:
[^1]: 《算法导论》【美】Tomas H.Cormen .etc 编著
