通过之前的介绍,我们知道了插入排序的原理。但是,如果一个元素距离它的正确位置非常远,那么我们就要做很多次大小比较,才能找出其正确位置。因此,其设计者希尔(Donald Shell),在插入排序的基础上,提出了一种更高效的改进版本–希尔排序。
算法思想
文字描述起来比较复杂,下面直接看实例:
假设有数组 array = [80, 93, 60, 12, 42, 30, 68, 85, 10],先对其进行希尔排序。
1.选择步长step=4(len(arr)/2),根据步长进行分组(相同颜色代表一组)。
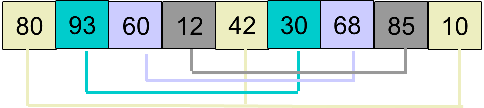
2.每组分别进行插入排序,得到下面的结果。
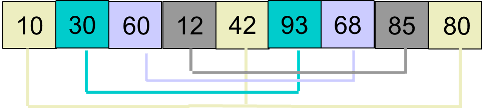
3.再次选择步长step=2(step/2),再次分组。
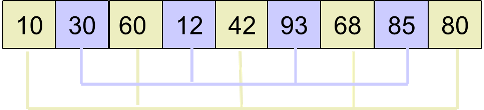
4.分别进行插入排序。
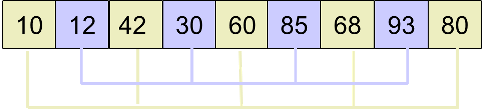
5.step=1(step/2),此时,在最后进行插入排序即可。
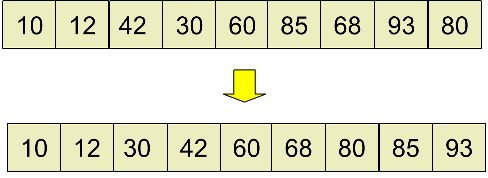
备注:同样还是使用插入排序,但是由于在前面的几步分组、排序的过程中,已经把一个可能原来“很无序”的数组,逐步地变成了一个“比较有序”的数组,最后进行微调即可。我们知道一个数组越有序,对其进行插入排序的效率就越高,希尔排序实际上解决的就是如何把可能非常无序的数组通过一系列操作,变得比较有序,这时,再使用插入排序就比较高效了。
注意
步长的选择
shell算法的性能与所选取的分区长度序列有很大关系。我们通常把步长取半直到步长达到1。
已知的最好步长序列是由Sedgewick提出的(1, 5, 19, 41, 109,…),该序列的项来自94^i - 9 2^i + 1和2^{i+2} * (2^{i+2} - 3) + 1这两个算式。这项研究也表明“比较在希尔排序中是最主要的操作,而不是交换。”用这样步长序列的希尔排序比插入排序和堆排序都要快,甚至在小数组中比快速排序还快,但是在涉及大量数据时希尔排序还是比快速排序慢。
时间复杂度
希尔排序的时间复杂度分析很复杂。总之可以证明,其最坏情况下的时间复杂度是 O(n^2) ,但是对希尔排序稍加一点改进,就可以使其时间复杂度提高到 O(n^1.5) 。
实现
1 | def ShellSort(arr): |
