为了介绍堆排序这种算法,我们先总结一下堆这种数据结构。
优先队列
我们都知道队列(Queue)这种先进先出(FIFO)的数据结构。队列还有一种变体叫做“优先队列”(Priority Queue)。
优先队列的出队(Dequeue)操作和队列一样,都是从队首出队。但在优先队列的内部,元素的次序却是由“优先级”来决定:高优先级的元素排在队首,而低优先级的元素则排在后面。这样,优先队列的入队(Enqueue)操作就比较复杂,需要将元素根据优先级尽量排到队列前面。
我们很自然地会想到用之前学的排序算法和队列的方法来实现优先队列。但是,在列表里插入一个元素的时间复杂度是O(n),对列表进行排序的时间复杂度是O(nlogn)。其实可以用别的方法来降低时间复杂度。一个实现优先队列的经典方法便是采用二叉堆(Binary Heap)。二叉堆能将优先队列的入队和出队复杂度都保持在O(logn)。
二叉堆
堆的性质:父节点的键值总是大于或等于(小于或等于)任何一个子节点的键值。
二叉树的性质:除了最底层,该树是完全充满的。而且是从左向右填充。
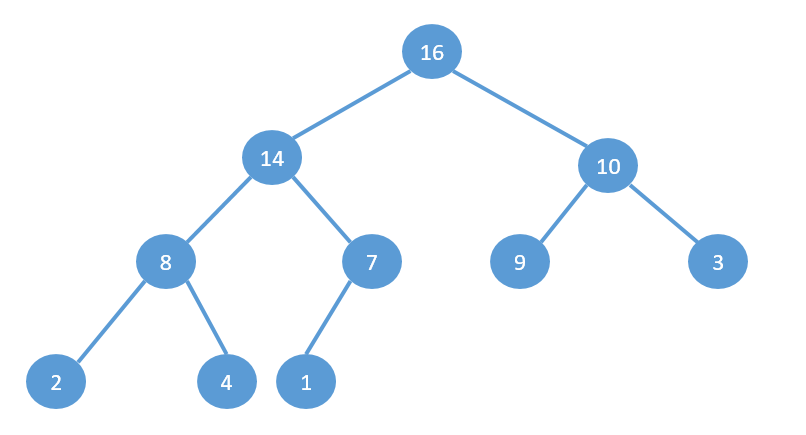
二叉堆的性质:二叉堆是完全二叉树或者是近似完全二叉树。当父节点的键值大于或等于它的每一个子节点的键值时我们称它为最大堆,反之称之为最小堆。可以看出它兼具堆和二叉树二者的性质。
下图就是一个最大堆:
二叉堆是用数组实现的,我们注意一点,通常为了方便二叉堆的操作,我们在数组的第一个元素a[0]中是不存放堆的元素的,我们习惯从1开始对这个堆进行编号,如下图所示:
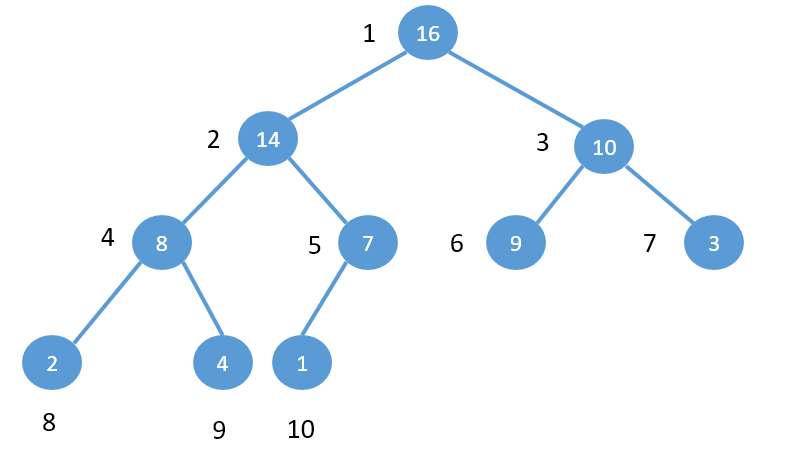
我们可以发现这样的规律:
1.PARENT(i)=i/2
2.LEFT(i) = 2*i
3.RIGHT(i) = 2*i+1。
基本操作
二叉堆的基本操作中最重要的一点就是,不管如何操作,要随时维护这个堆。最基本的两个操作为:shift up和shift down。
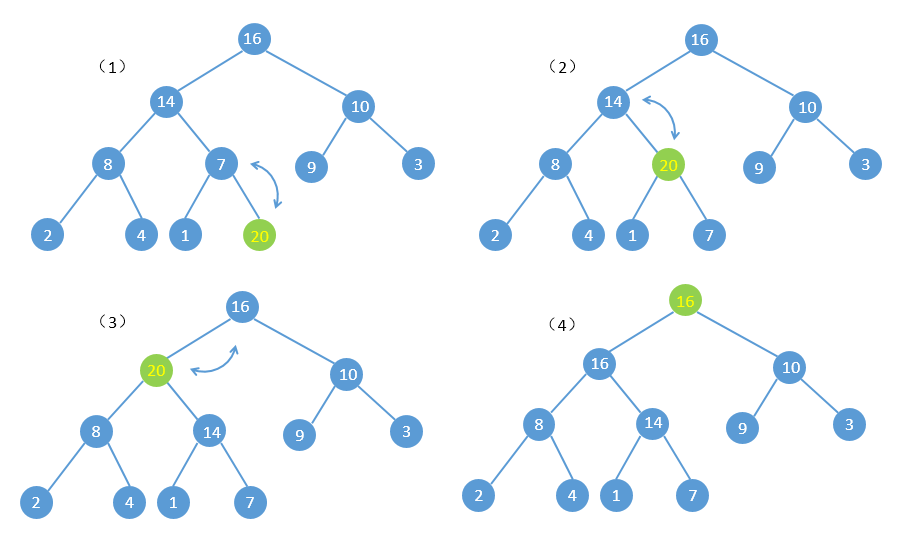
插入
在插入操作的时候,会破坏上述堆的性质,所以需要进行shift up的操作,来维护这个堆,实际上就是不停的交换,例如,在上面的最大堆的基础上插入20这个数,具体过程如下:
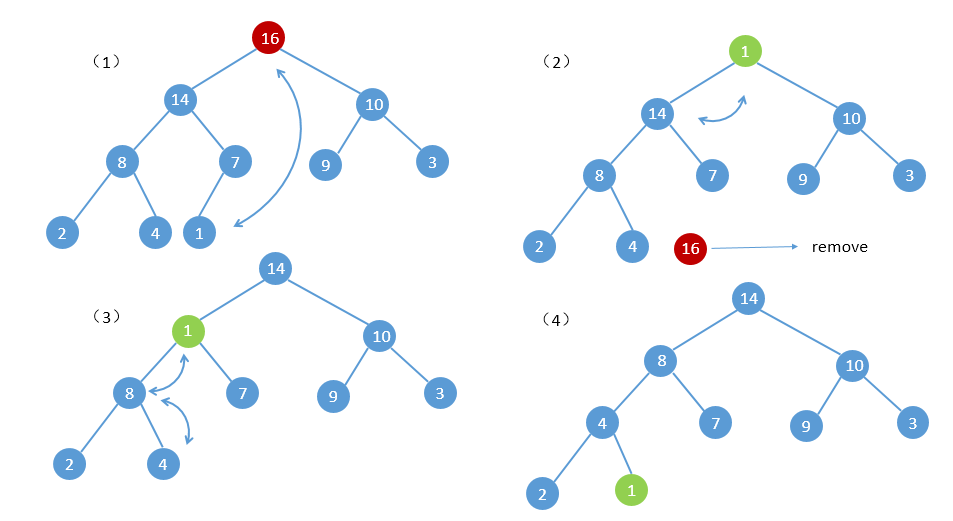
删除
在删除操作的时候,也会破坏上述堆的性质,所以需要进行shift down的操作。删除操作先是待删元素和末尾元素交换,末尾元素依次进行shift down操作,还是上面的例子,具体过程如下:
实现二叉堆
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
|
class BinaryHeap(object):
def __init__(self):
self.item_list = [0]
def insert(self, new_item):
self.item_list.append(new_item)
self.item_list[0] += 1
self.shiftup(self.item_list[0])
def shiftup(self, index):
while index/2 > 0:
if self.item_list[index] < self.item_list[index/2]:
temp = self.item_list[index]
self.item_list[index] = self.item_list[index/2]
self.item_list[index/2] = temp
index = index/2
else:
break
def get_min(self):
if self.item_list[0]>0:
return self.item_list[1]
else:
return None
def pop_min(self):
if self.item_list[0] == 0:
return None
else:
top_min = self.item_list[1]
self.item_list[1] = self.item_list[self.item_list[0]]
self.item_list[0] -= 1
self.shiftdown(1)
return top_min
def shiftdown(self, index):
while 2*index <= self.item_list[0]:
if 2*index+1 <= self.item_list[0]:
if self.item_list[2*index]<self.item_list[2*index+1]:
if self.item_list[index]>self.item_list[2*index]:
temp = self.item_list[index]
self.item_list[index] = self.item_list[2*index]
self.item_list[2*index] = temp
index = 2*index
else:
break
else:
if self.item_list[index]>self.item_list[2*index+1]:
temp = self.item_list[index]
self.item_list[index] = self.item_list[2*index+1]
self.item_list[2*index+1] = temp
index = 2*index+1
else:
break
else:
if self.item_list[index]>self.item_list[2*index]:
temp = self.item_list[index]
self.item_list[index] = self.item_list[2*index]
self.item_list[2*index] = temp
else:
break
def isEmpty(self):
return 0 == self.item_list[0]
def size(self):
return self.item_list[0]
def build_heap(self, input_list):
self.item_list = [0]+input_list
self.item_list[0] = len(input_list)
for index in range(self.item_list[0]/2, 0, -1):
self.shiftdown(index)
|