并查集（Union-Find）是用于解决动态连通性类问题的一种数据结构。

动态连通性问题

动态连通性问题是一个非常基础的计算性问题，而且它在现实世界中的应用很广泛，庞大的电脑网络、数以亿计的社交网络中的人类、数学集合中的元素、计算机程序中的变量、照片中的像素，都会涉及到动态连通性。

1.这类问题的输入是一列整数对，每个整数都表示一个某种类型的对象，一对整数“p q”表示的含义是“p和q相连”。

2.“相连”是一种等价关系
1） 自反性（p与p相连接）；
2） 对称性（若p连接到q，那么q也连接到p）；
3） 传递性（若p连接到q，q连接到r，则p连接到r）。

3.等价关系将对象分成多个等价类，它们构成多个集合，称为“连通组件”（Connected Components）。

并查集

对于一组数据，并查集主要支持两个动作，回答一个问题。

动作

1.union(p,q)：将p,q连接。
2.find(p)：查找p。

问题

isConnected(p,q)：检测p,q是否连接并返回布尔值。

举个例子：

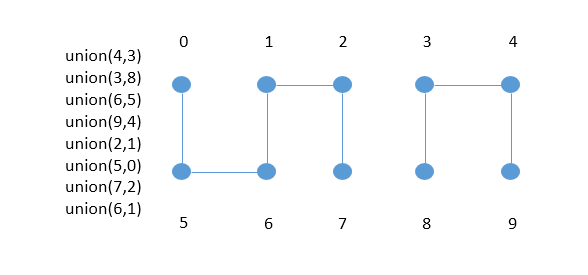
我们可以通过union操作，实现上图的连接，形成了两个连通分量，或称为一个组。

实现

Quick-Find实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
id = []
count = 0

def unionFind(n):
    count = n
    for i in xrange(count):
        id[i] = i

def isConnected(p,q):
    return find(p) == find(q)

def find(p):
    return id[p]

def union(p, q):
    pid = find(p)
    qid = find(q)

    for i in xrange(count):
         if id[i] == pid:
             id[i] = qid

备注：上面的实现，只给出了每个函数的实现，其中，有一点需要说明，就是id这个数组。初始化时，每个元素都是指向自己，union操作时，循环遍历id数组，将qid指向pid这条链上的最后一个元素。

具体过程如下所示：

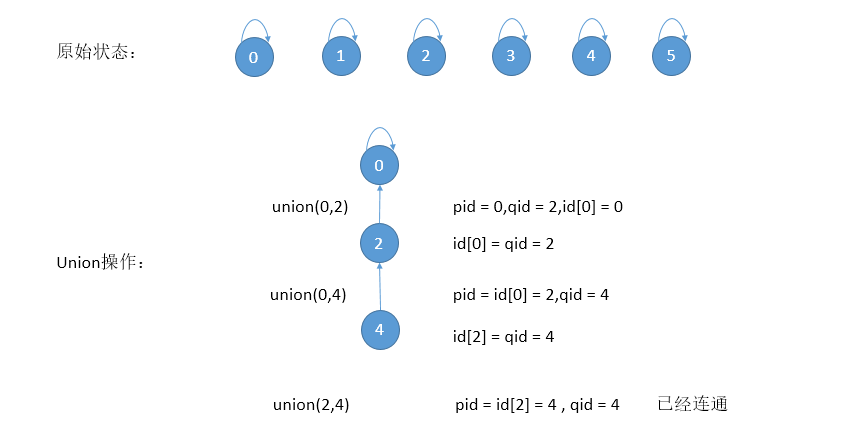
Quick-Union实现

上面的Quick-find实现在规模增大时，会面临性能问题，其主要来源是union操作需要遍历数组，为了改善性能，需要避免执行union操作时遍历数组，Quick-Union实现达到了这一目的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
parent = []
count = 0

def unionFind(n):
    count = n
    for i in xrange(count):
        parent[i] = i

def isConnected(p,q):
    return find(p) == find(q)

def find(p):
    while p!=parent[p]:
        p = parent[p]
    return p

def union(p, q):
    proot = find(p)
    qroot = find(q)

    if proot != qroot:
        parent[proot] = qroot

具体过程如下所示：

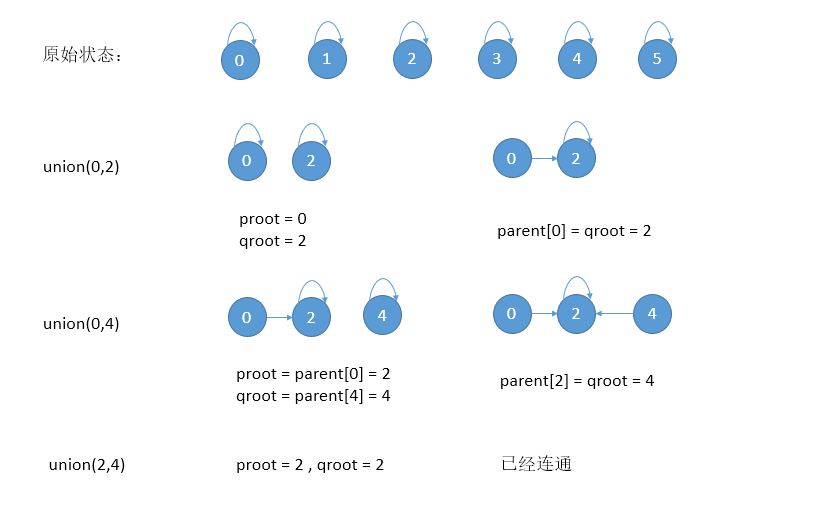
Quick-Union优化

基于元素个数优化

引入一个num[i]，用来记录以i为根的集合中元素个数。

1
2
3
4
5
6
7
num = []

def unionFind(n):
    count = n
    for i in xrange(count):
        parent[i] = i
        num[i] = 1

始终保持元素少的根节点指向元素多的根节点，这样有很大的概率可以维护树的高度增长的不是那么快。

1
2
3
4
5
6
7
8
9
10
11
def union(p, q):
    proot = find(p)
    qroot = find(q)

    if num[proot] < num[qroot]:
        parent[proot] = qroot
        num[qroot] += num[proot]

    else:
        parent[qroot] = proot
        num[proot] += num[qroot]

基于rank的优化

在上述的优化过程中，只是有很大的概率可以维护树的高度增长的不是那么快。实际上并不准确，更多的时候我们采用的是基于rank的优化。

1
2
3
4
5
6
7
rank = []

def unionFind(n):
    count = n
    for i in xrange(count):
        parent[i] = i
        rank[i] = 1

和上面一种优化相比，区别在于，这里维护的是真正的树的深度，树深小的指向树深大的，只有当相等的时候树深才会加1。

1
2
3
4
5
6
7
8
9
10
11
def union(p, q):
    proot = find(p)
    qroot = find(q)

    if rank[proot] < rank[qroot]:
        parent[proot] = qroot
    elif rank[qroot] < rank[proot]:
        parent[qroot] = proot
    else:
        parent[proot] = qroot
        rank[qroot] += 1

路径压缩（Path Compression）

先实现第一种路径压缩优化，实际上只需要对find(p)进行一个修改：

1
2
3
4
5
def find(p):
    while p!=parent[p]:
        parent[p] = parent[parent[p]]
        p = parent[p]
    return p

具体过程如下：

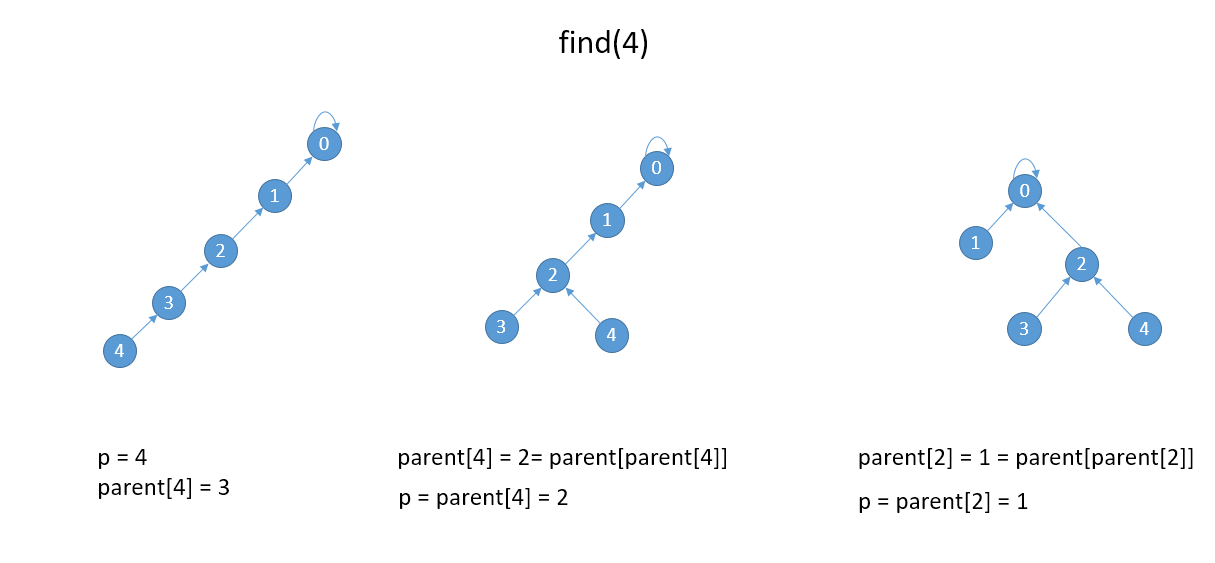
可以看到，路径的确被压缩了，但是这仍然不是最优的压缩路径，最优的情况下是如下图这种压缩方式：

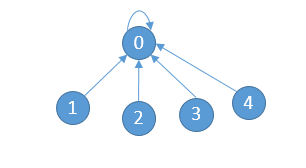
使用递归实现：

1
2
3
4
def find(p):
    if p!=parent[p]:
        parent[p] = find(parent[p])
    return p

以上内容，便是并查集的内容，后续会更新一些笔面试题目，加深应用和理解。